Review of Linear Regression

Suppose $X$$X$ is $n\times p$$n\times p$ with n observations and p features. Then we have two views in the space for the Linear Regression. The first one is from ${\mathbb{R}}^p$$\R^p$ space, where each observation $(x_{i1},\dots ,x_{ip},y_i)$$\left(x_{i 1}, \ldots, x_{i p}, y_{i}\right)$ is a point.

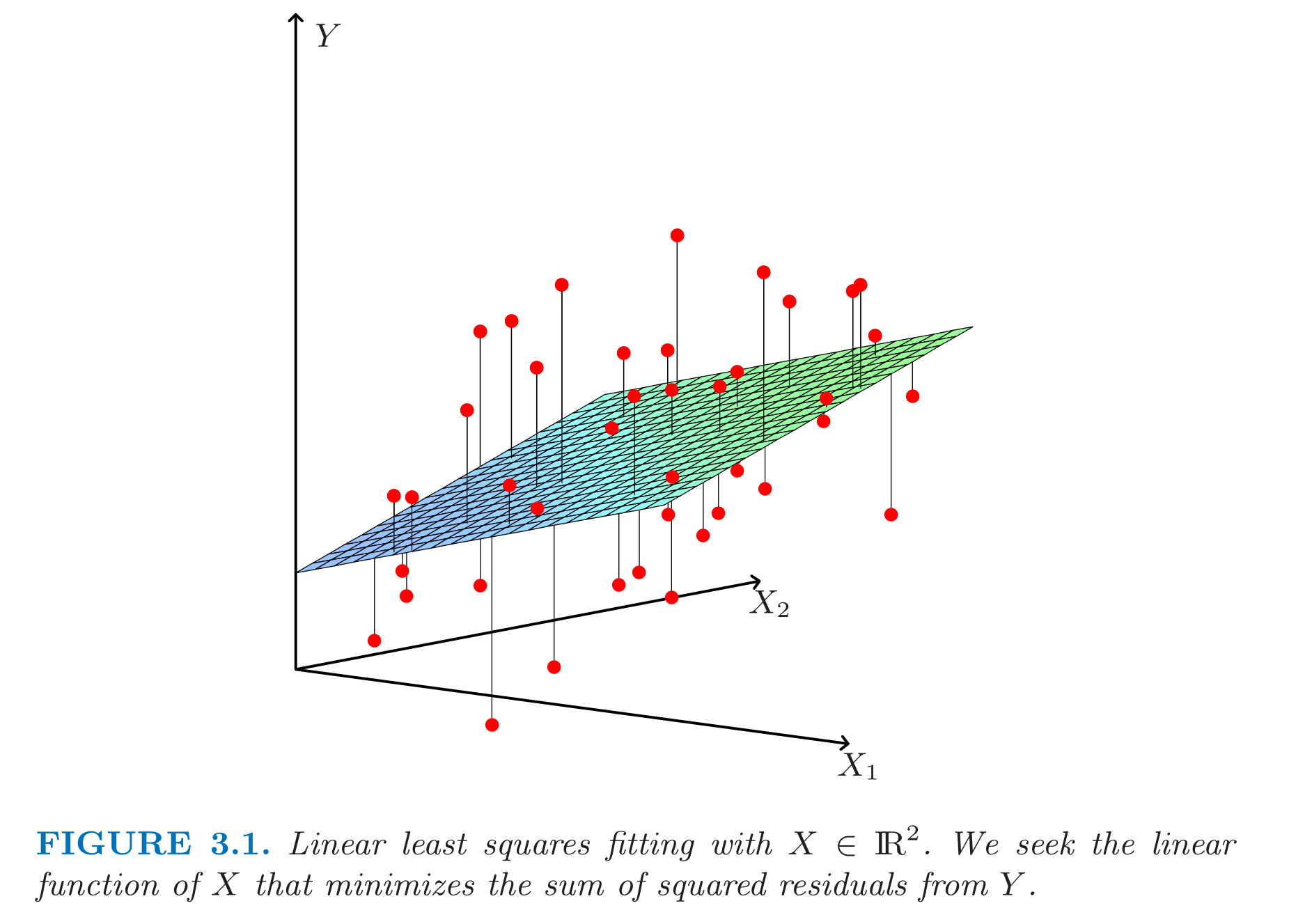
The second view is having each column (feature) as vectors in ${\mathbb{R}}^N$$\R^N$ space.

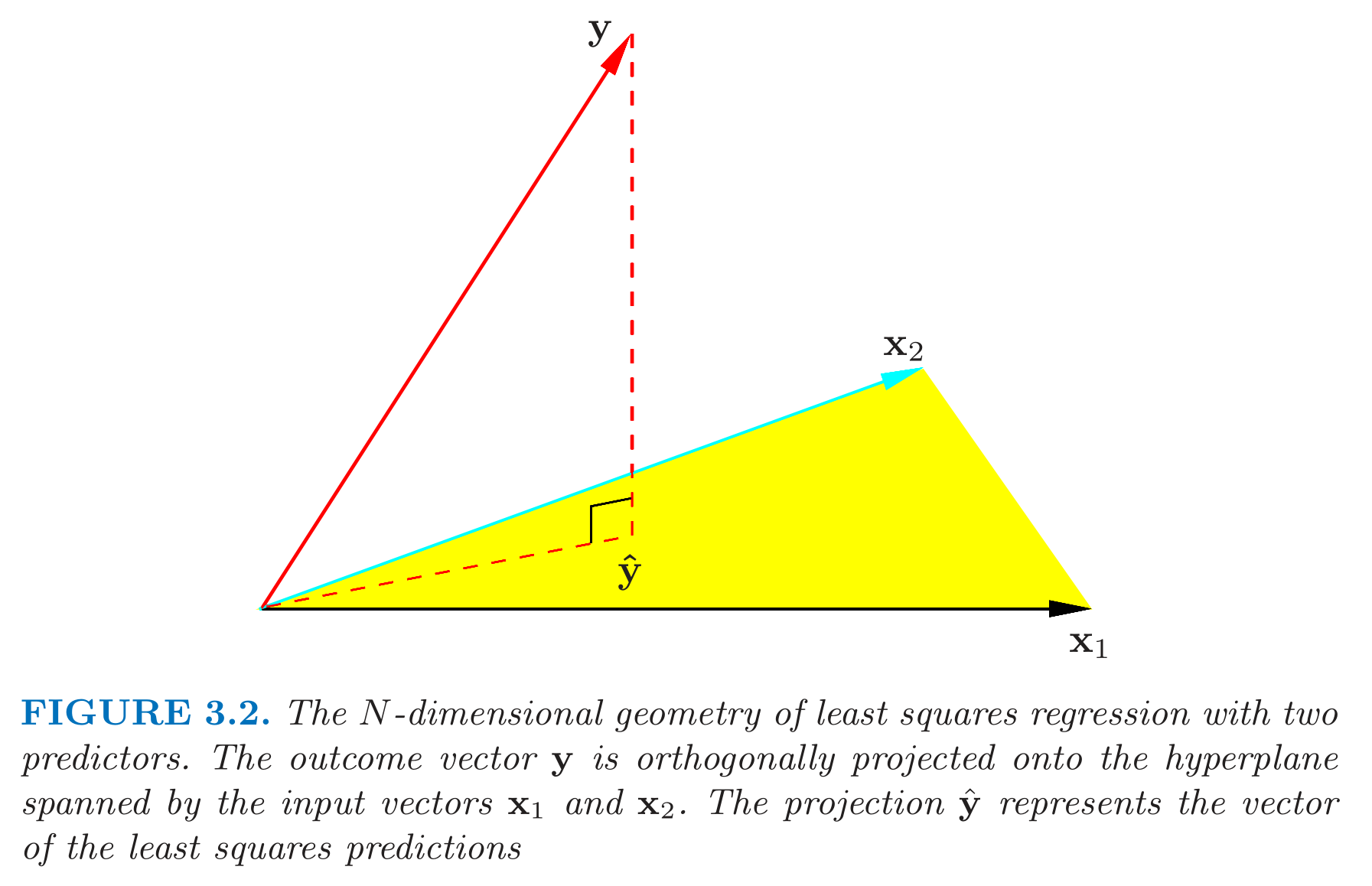
The orthogonal projection is done by the matrix $H$$H$, which linearly transforms $Y$$Y$ to $\hat{Y}$$\hat{Y}$ on the hyperplane spanned by $X$$X$, the features.

Statistics and Machine Learning

• Inference: Ask questions about $f(x)$$f(x)$.
• Interpretability: Ask questions about $\hat{f}(x)$$\hat{f}(x)$
• Prediction: Guess $Y$$Y$ using $\hat{f}(X)$$\hat{f}(X)$.

在传统的统计学中, 我们更关注inference, 需要对beta系数的variance, 显著性, confidence interval等有要求, 这个时候类似collinearity的问题就需要解决. 但是在prediction问题中, 我们则不需要考虑这个问题. 有时候即便model是错误的, 也并不影响其在某个范围有较好的预测性.

Linear Regression in Higher Dimensions

在homework中做过一个simulation. 当$Y=4X_1+ϵ$$Y=4X_1+\epsilon$这个true model保持不变的情况下, 我们增加一些无效的变量$X_n$$X_n$, 会导致整个模型的MSE随着无效变量的增多而呈现指数型的增加. 要解决这个问题, 需要引入ridge和lasso这类模型. 出发点是, 牺牲一部分bias来换取variance的降低.

由于OLS已经是Best Linear Unbiased Estimator, 在unbiased的估计量中, 已经给出了minimum variance. 我们为了降低整体的prediction error, 只能牺牲掉unbiased这个属性.

Bias and Variance

$$\mathrm{bias}(\hat{\mu }(x))=\mathbb{E}[\hat{\mu }(X)\mid X=x]-\mu (x)$$

Bias: Error in the expectation of our estimator. Does not depend on the randomness of our particular training data realization, just the flexibility of our function. Making $\hat{\mu }$$\hat{\mu}$ more flexible usually decreases bias.

$$\mathrm{var}(\hat{\mu }(x))=\mathbb{E}[(\hat{\mu }(X)-\mathbb{E}[\hat{\mu }(X)\mid X=x]{)}^2\mid X=x]$$

Variance: Error from the variance of our estimator around its mean. Does not depend on the true function $\mu$$\mu$ ! Tends to increase with the flexibility of $\hat{\mu }$$\hat{\mu}$, since a change in data has more effect.

Ridge Regression

To solve the problem of higher dimensions, and reduce the variance of the model by adding the bias, we can introduce a penalty term to the cost function. A cost function could punish more when coefficients are larger, and drives the coefficients much towards zero.

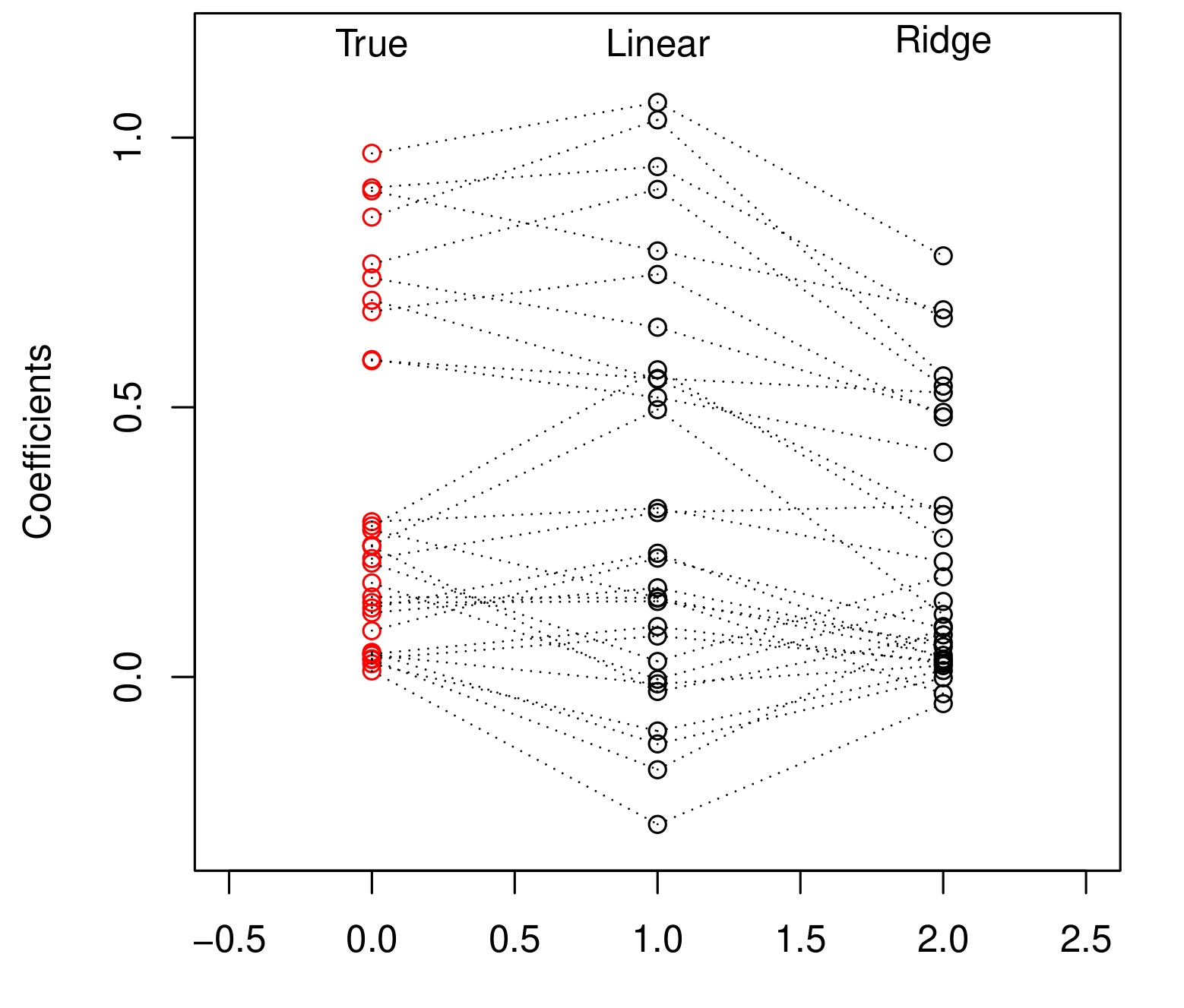
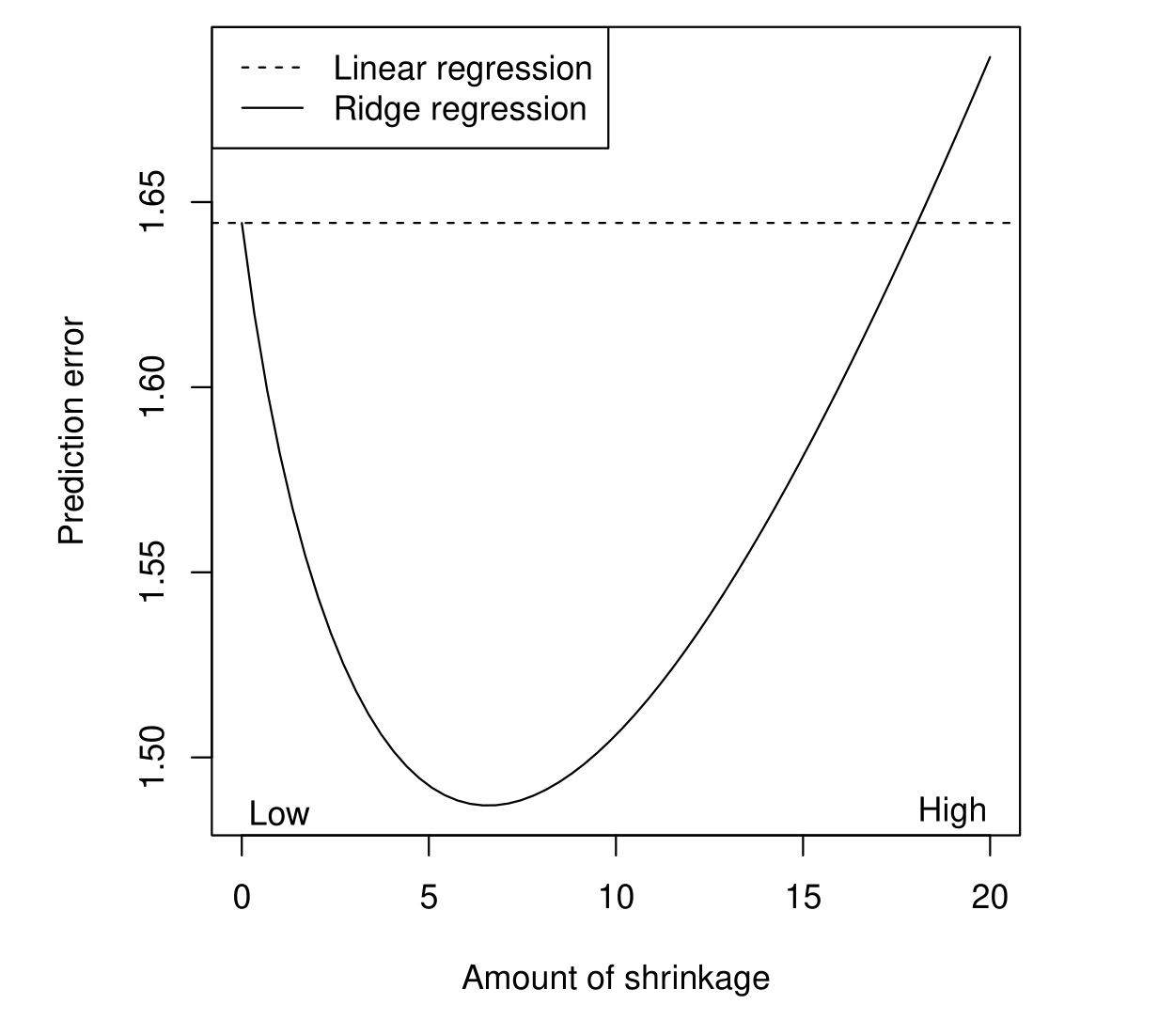
上面两幅图可以看到ridge对coefficients作了shrinkage, 从而降低model的variance.

• 当lambda = 0的时候, 等价于OLS
• 当lambda = infinity的时候, 所有的系数都趋近于0.

特别注意, 只要存在lambda, 那么一定会削弱model在training set上的MSE表现, 只是可能在prediction上表现更好.

Centering and Scaling

• Centering: to avoid penalty on the intercept term.
• Scaling: to avoid imbalanced penalty due to the magnitude of the coefficients.

一般而言, 我们不希望这个shrinkage effect发生在intercept上. 所以假如我们将intercept这一项从beta向量中剔除, 那么我们的目标function变成了.

如果$X$$X$的columns被center过, 那么${\beta }_0=\overline{y}$$\beta_0=\bar y$. (因为regression line一定会通过$\overline{x},\overline{y}$$\bar x, \bar y$. 如果$Y$$Y$也被center过, 那我们不再需要intercept项. 所以实际当中, 通常需要将X和Y都中心化, 减去mean, 这样也会让推导容易很多.

更重要的是, 在ridge中, 所有的predictors需要scaling. 原因是$\parallel \beta {\parallel }_2^2=\sum _{j=1}^p{\beta }_j^2$$\|\beta\|_{2}^{2}=\sum_{j=1}^{p} \beta_{j}^{2}$ is unfair if the variables are not measured in the same units. Scale the X to have sample variance 1.

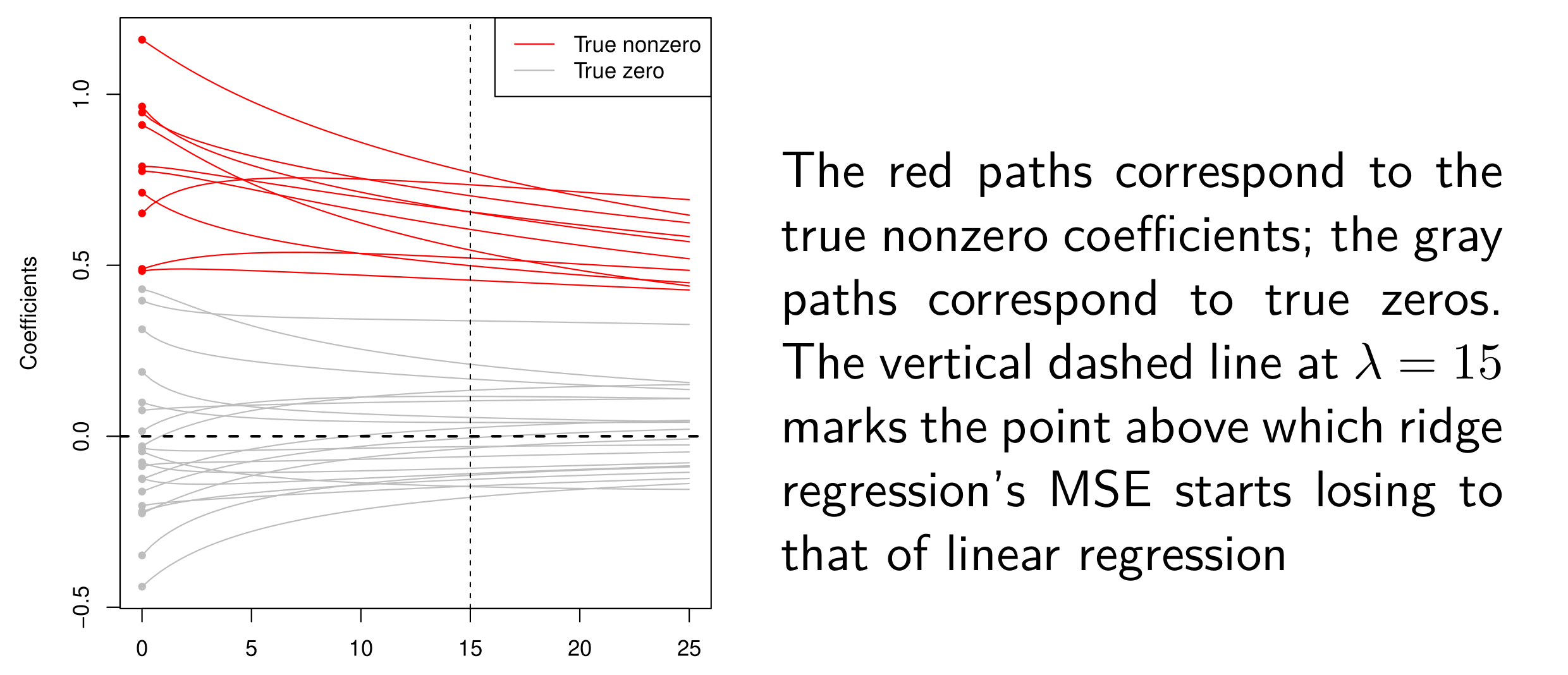
Ridge的缺陷也很明显, 上图表示两类coefficients, 一类是true value = 0, 另一类是nonzero. Ridge的penalty大部分作用在了那些nonzero的coefficients上, 当lambda逐渐增大的时候, 我们关注的coefficients收到了很大的影响, 但是这些本该是zeros的coefficients基本停滞了.

Lasso

Lasso adds a $l_1$$l_1$ penalty (the absolute value of the coefficients) to the cost function.

$l_1$$l_1$ penalty的特性导致Lasso可以将一些coefficients压缩到0, 这是ridge办不到的.

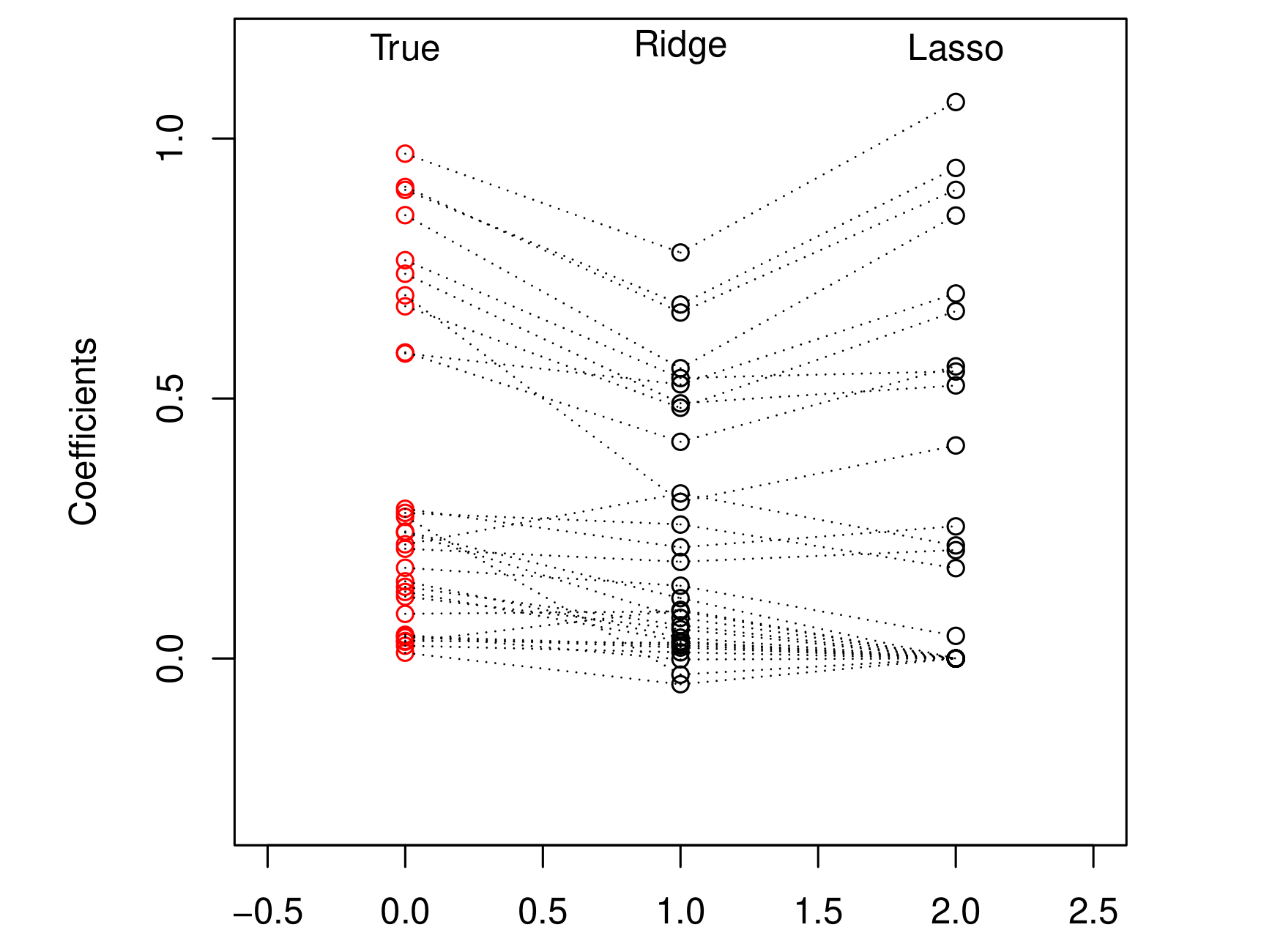
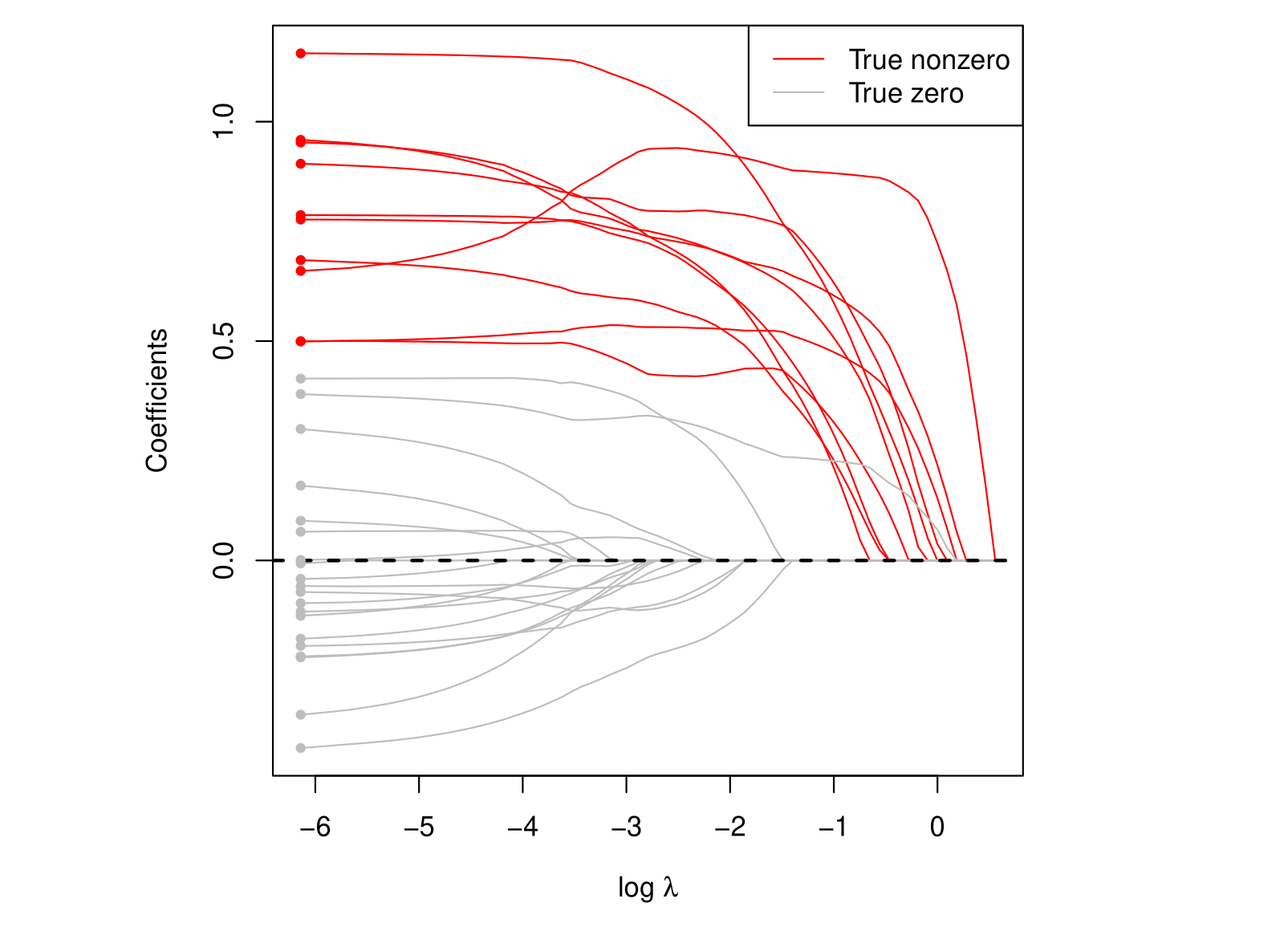
我们发现, 那些true values = 0的coefficients确实被压缩到了0, 这是我们愿意看到的结果. 我们将这种一部分coefficients变成零的情况，叫做sparsity。这有助于帮助我们得到以下特性,

1. interpretability - understanding $\hat{f}$$\hat f$.
2. measure few things in the future, lower computation costs
3. Know the underlying data. What features are useful?

和之前的ridge regression一样, 我们也需要做centering和scaling.

Ridge and Lasso Comparison

To understand further why different penalty forms can lead to different behaviors, think about the following simplified problem. If we put $X=I$$X = I$ an orthogonal matrix. Then and OLS will give us the solutions of $\hat{\beta }=Y$$\hat{\beta}=Y$. The following analysis will give insights for Ridge and Lasso.

Ridge has a direct solution by taking the derivatives. The size of beta, compared with OLS betas, are smaller, and can never be zero.

For Lasso, ${\beta }_i$$\beta_i$ depends on the minimization of ${(y_i-{\beta }_i)}^2+\lambda \left|{\beta }_i\right|$$\left(y_{i}-\beta_{i}\right)^{2}+\lambda\left|\beta_{i}\right|$.

这个表达式求导之后, 会得到一个分段函数. 当$y_i\in [-\frac{\lambda }{2},\frac{\lambda }{2}]$$y_i\in[-\frac{\lambda}{2},\frac{\lambda}{2}]$之间的时候, beta = 0, 除此以外的其他情况, beta都被压缩或者提升了$\frac{\lambda }{2}$$\frac{\lambda}{2}$. 所以, 当OLS的beta(也就是这里的$y_i$$y_i$)越小的时候, 它更有可能被挤压到0.